Mathematics is often described as the language of the universe, and understanding the implications of numbers can lead us to fascinating insights and applications in various fields. In this article, we delve into the concept of using 3.4 as a root in mathematics, exploring its mathematical implications and its applications in technology and software development, specifically in the context of APIs and platforms such as APIPark and the Amazon API Developer Portal.
Table of Contents
- Introduction to Roots in Mathematics
- Understanding 3.4 as a Root
- Mathematical Implications of 3.4 as a Root
- Applications in Software Development
- 4.1 Overview of APIPark
- 4.2 Utilizing the Amazon API Developer Portal
- Advanced Identity Authentication with APIs
- Conclusion
1. Introduction to Roots in Mathematics
In mathematics, a root of a number ( x ) refers to a value ( r ) such that ( r^n = x ), where ( n ) is a positive integer. The most commonly known root is the square root, represented as ( \sqrt{x} ). However, roots can extend beyond squares; for example, the cube root ( \sqrt[3]{x} ) or fourth root ( \sqrt[4]{x} ).
The concept of a number as a root also applies in the realm of higher mathematics, including algebra and calculus. When exploring the implications of a number like 3.4 as a root, we can assess its properties, implications, and real-world applications.
2. Understanding 3.4 as a Root
When we refer to 3.4 as a root, we can consider several mathematical expressions. For example, if we declare 3.4 as the cube root of ( x ), we express it as:
[
3.4 = \sqrt[3]{x}
]
This equation implies that:
[
x = 3.4^3
]
Calculating ( 3.4^3 ):
[
3.4^3 = 3.4 \times 3.4 \times 3.4 = 39.304
]
Thus, 3.4 serves as the cube root of 39.304. Continuing this process, we establish that 3.4 can be utilized in various polynomial expressions, providing foundational insights that can be utilized in different mathematical contexts.
3. Mathematical Implications of 3.4 as a Root
The implications of defining 3.4 as a root can be far-reaching. Here are a few key considerations:
-
Numerical Analysis: In numerical methods, understanding the roots of equations allows developers and mathematicians to find solutions to polynomial functions.
-
Function Behavior: Analyzing the significance of ( 3.4 ) as a root can help determine the behavior of specific functions, particularly when examining curve intersections or root-finding algorithms, important in calculus and optimization.
-
Data Modeling: In data science, defining root values leads to better data fitting techniques, especially for power models or regression analyses.
-
Real-World Scenarios: Engineers and physicists might determine certain values needed to stabilize structures or understand wave functions based on polynomial roots.
4. Applications in Software Development
The mathematical concept of roots, such as 3.4, also extends into software development, particularly when it comes to APIs. APIs, or Application Programming Interfaces, allow software programs to communicate and exchange data.
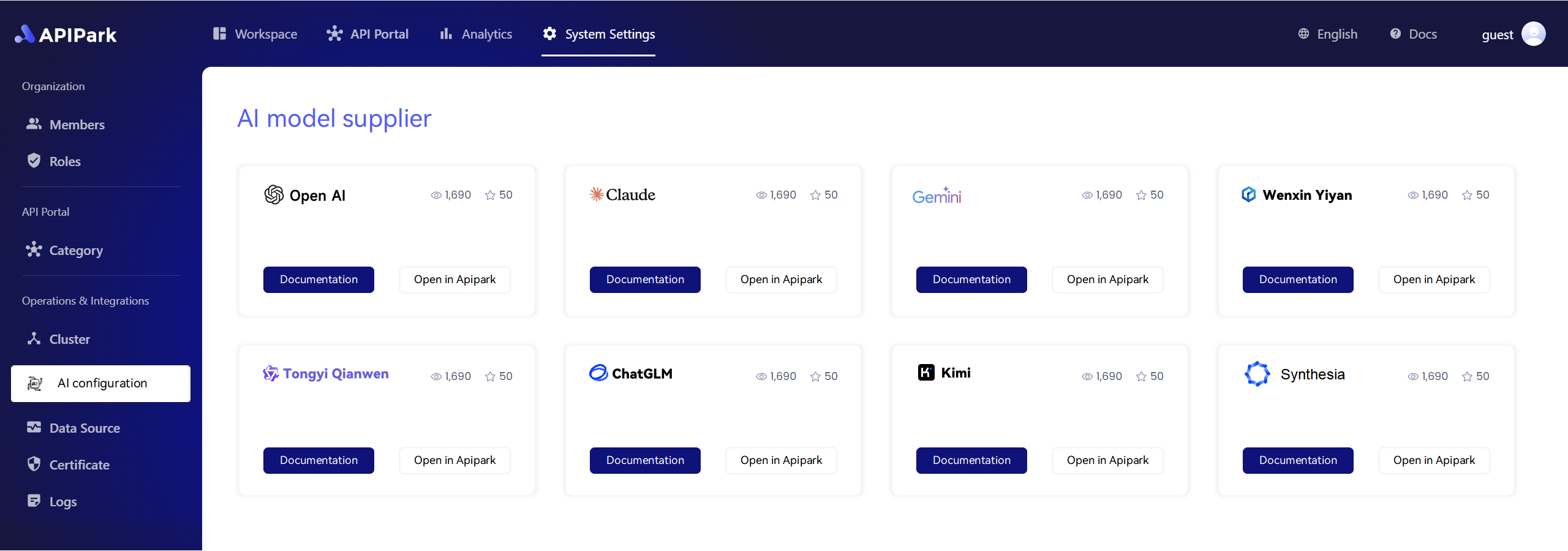
4.1 Overview of APIPark
APIPark is a powerful API management tool designed to help organizations streamline their API usage. This tool allows for easy management of API services, providing centralized control over API endpoints, authentication, and lifecycle management.
By applying mathematical principles, including the understanding of roots like 3.4 in optimization algorithms, developers can enhance the efficiency and performance of API calls.
Key Features of APIPark:
| Feature | Description |
|---|---|
| Centralized API Management | Allows easy oversight and organization of multiple APIs |
| Lifecycle Management | Manage API versions from creation to sunset |
| Multi-Tenant Support | Isolate resources for different clients or departments |
| Approval Workflows | Ensures compliance through an approval process for API usage |
| Detailed Logging | Tracks API usage and performance to resolve issues quickly |
4.2 Utilizing the Amazon API Developer Portal
Amazon’s API Developer Portal is an essential resource for developers looking to integrate with Amazon’s services. Understanding ( 3.4 ) as a root allows developers to create robust applications that interact seamlessly with Amazon’s API offerings.
In practice, utilizing mathematical algorithms similar to root analysis can lead to better resource allocation and improved API performance. For example, one might analyze response times and resource usage, finding optimal values that eliminate bottlenecks in data processing.
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
5. Advanced Identity Authentication with APIs
As the landscape of technology evolves, so does the need for security, especially in API environments. Advanced Identity Authentication enables developers to secure access to sensitive APIs effectively.
Key Considerations for Advanced Authentication:
- Token Management: Understanding token expiration and renewal as mathematical functions can significantly enhance security protocols.
- Access Control: Implementing mathematical models to define user roles and permissions allows for a granular approach to API security.
By integrating robust authentication strategies with a mathematical understanding of roots, developers can enhance their API security while maintaining efficient access pathways.
6. Conclusion
The exploration of 3.4 as a root opens a myriad of mathematical implications and applications, particularly within the realms of software development and API management. Understanding how to leverage this knowledge can positively impact the performance and security of APIs in platforms like APIPark and the Amazon API Developer Portal.
Incorporating mathematical principles into software design aids in creating efficient systems, ultimately leading to better user experiences, robust applications, and secure environments that foster innovation. As technology continues to evolve, so will the applications of these mathematical concepts, ensuring that developers remain equipped to meet future challenges.
In conclusion, understanding numbers like 3.4 not only enriches our mathematical knowledge but also empowers us in the fields of engineering, data science, and software development, grounding our technological advancements in solid mathematical foundation.
This article has covered the concept of 3.4 as a root, its mathematical implications, and applications in the context of software development, highlighting significant tools like APIPark and the Amazon API Developer Portal. It represents just one of the many ways mathematics intertwines with technology and practical problem solving.
🚀You can securely and efficiently call the OPENAI API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
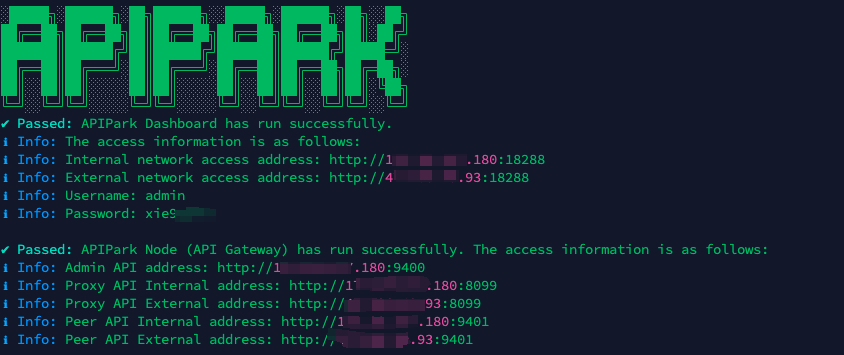
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
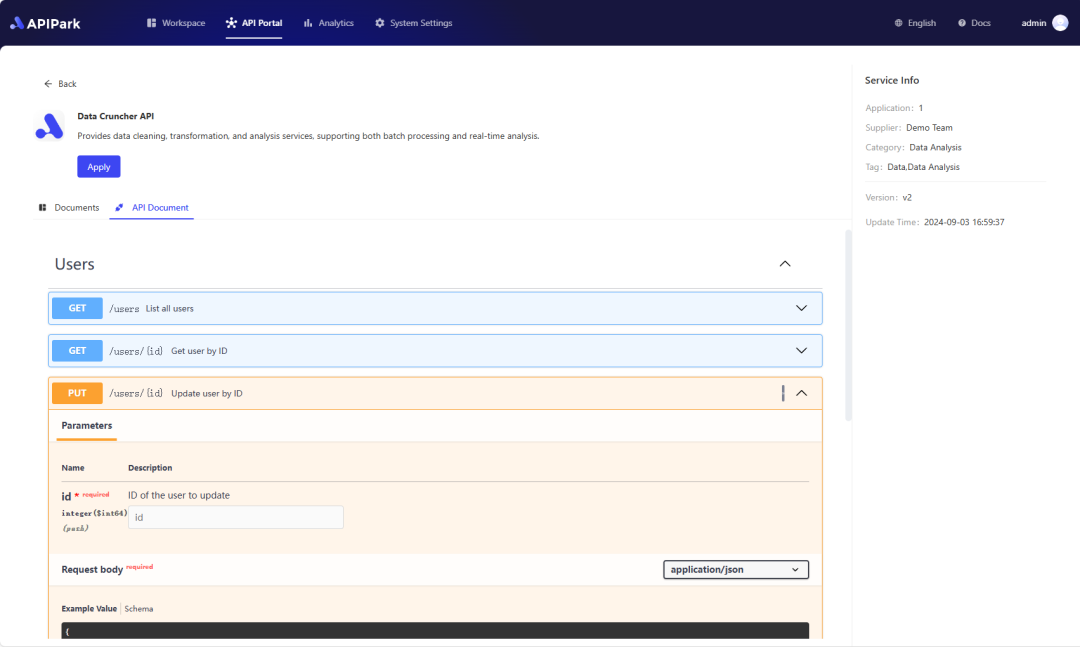
Step 2: Call the OPENAI API.