Algebra is a key branch of mathematics that includes the study of mathematical symbols and the rules for manipulating these symbols. Among various algebraic concepts, the notion of roots plays a crucial role, particularly when examining equations and functions. In this guide, we will dive deep into understanding 3.4 as a root, while also discussing the intersection of technology through platforms like AI Gateway, Apigee, and Traffic Control for better API management.
What is a Root in Algebra?
In mathematical terms, a root is a solution to an equation that can be expressed as:
[ f(x) = 0 ]
For example, the equation ( x^2 – 4 = 0 ) has roots x = 2 and x = -2 because substituting those values into the equation results in zero. Roots can be real or complex numbers, depending on the nature of the polynomial.
Understanding roots is fundamental because they serve various purposes, such as solving equations, optimizing functions, and analyzing graphs.
3.4 as a Root: An Example
When we say 3.4 as a root, we generally imply that 3.4 is a solution to a specific algebraic equation. Let’s consider the simple polynomial equation:
[ f(x) = x – 3.4 = 0 ]
To find the root, we look for the value of x that satisfies this equation:
[ x = 3.4 ]
This means that when we substitute 3.4 back into the function, the equation equals zero:
[ f(3.4) = 3.4 – 3.4 = 0 ]
In this case, 3.4 is indeed a root of the function. By understanding this concept, we realize that roots help us uncover the behavior of functions and their intersections with the x-axis.
Practical Implications of Roots
Roots are not just theoretical but have real-world applications in fields such as engineering, physics, and economics. For example, in physics, solving for roots can help determine the points at which an object’s trajectory intersects with a specified height.
The Intersection of Algebra and Technology
Leveraging AI Gateway and Apigee
As we explore the mathematical concept of roots, the realm of technology offers tools like the AI Gateway and Apigee to manage and optimize API services. The mathematical principles of managing data make their way into how we monitor and control API traffic.
Here’s how:
- AI Gateway: This platform can enhance API management, making computations and data retrieval more efficient. Similar to how we find roots in algebra to optimize performance, AI Gateways streamline data flows to pinpoint issues within APIs.
- Apigee: A product of Google Cloud, Apigee enables developers to create, secure, and analyze APIs. In situations where managing API traffic is akin to solving for roots, Apigee helps companies manage their digital landscapes effectively.
Traffic Control of APIs
As organizations increasingly rely on APIs for inter-service communication, controlling traffic is essential. Proper traffic management ensures that applications remain responsive and resilient, especially during peak loads.
Table 1: Comparing AI Gateway, Apigee, and Traffic Control Features
| Feature | AI Gateway | Apigee | Traffic Control |
|---|---|---|---|
| API Analytics | Yes | Yes | Limited |
| Request Throttling | Yes | Yes | No |
| Authentication | OAuth & JWT | OAuth 2.0, JWT | Basic Auth |
| Scalability | High | Very High | Medium |
| User Management | Basic | Advanced | N/A |
| Cost | Subscription-based | Usage-based | Free (Open Source) |
In the table above, we can see the differences that will help businesses choose the right solution depending on their needs and budget.
Mathematical Tools to Solve for Roots
To identify roots, mathematicians have created various methods, including:
- Factoring: Break down polynomials into simpler components.
- Graphing: Visualize functions to find intersections with the x-axis.
- Quadratic Formula: A standard application for finding roots of quadratic functions.
Graphical Representation of Roots
Using technology, we can also leverage graphical representations in software like Desmos or GeoGebra to visualize roots. For example, drawing the function ( f(x) = x – 3.4 ) highlights the intersection at ( x = 3.4 ).
Programming Example for Root Calculation
We can solve for roots programmatically using Python. Here is a Python code snippet to calculate the roots of a linear equation:
def find_root(a, b):
if a == 0:
raise ValueError("Coefficient 'a' cannot be 0.")
root = -b / a
return root
# Example Usage
a = 1 # Coefficient of x
b = -3.4 # Constant term
root = find_root(a, b)
print(f"The root of the equation {a}x + ({b}) = 0 is {root}")
This straightforward code allows us to find roots of any linear equation in the form ( ax + b = 0 ). The root calculated here will confirm the value, showcasing that 3.4 is, indeed, a solution.
Understanding the Broader Context
In summary, understanding roots like 3.4 as a root in algebra is essential for many mathematical applications. When combined with modern technology elements like AI Gateways, Apigee, and Traffic Control, we can efficiently manage data and address various challenges faced in computation and technology.
Through leveraging both algebraic principles and technological resources, we can lay the groundwork for future innovations.
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
Conclusion
Mastering the concept of roots in algebra, particularly with specific values such as 3.4, serves foundational and applied purposes. The ongoing convergence of algebra with technology through tools like AI Gateways and Apigee illustrates the far-reaching impacts that these concepts can have beyond pure mathematics. Whether for theoretical analysis or practical application, understanding the roots facilitates optimal decision-making processes and enhances operational efficiencies in various sectors.
By harnessing the power of both mathematics and technology, we enable future advancements and foster innovation across disciplines. This comprehensive guide serves as a stepping stone for further exploration into roots and their implications in both mathematics and technology.
Looking ahead, one can explore deeper topics such as polynomial roots, synthetic division for advanced polynomial equations, and complex roots, all of which can further enrich our understanding of the subject.
🚀You can securely and efficiently call the Gemni API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
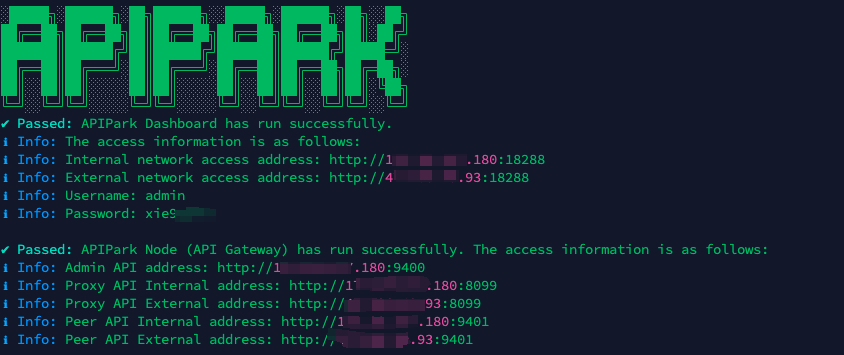
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
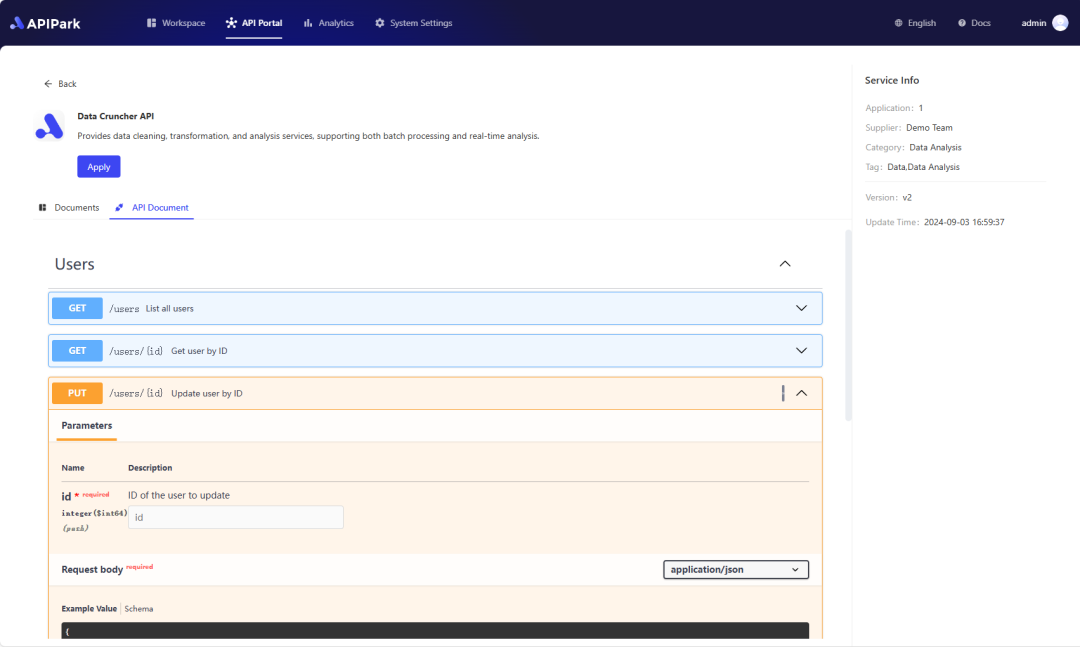
Step 2: Call the Gemni API.