Mathematics is a fascinating field that encompasses a myriad of concepts and theories. One such concept is that of the roots of numbers. In this article, we will delve deep into the significance of 3.4 as a root in mathematics, exploring its relevance in different mathematical contexts. Additionally, we will touch upon how technology, particularly using tools such as an AI Gateway and other resources like træfik and API, can enhance our understanding and application of these mathematical roots.
What Are Roots in Mathematics?
To grasp the significance of 3.4 as a root, it’s essential first to understand what roots are in mathematics. A root of a number is a value that, when multiplied by itself a certain number of times, gives that original number. For instance, the square root of 9 is 3 because 3 multiplied by itself (3 x 3) equals 9.
The mathematical notation for a root is denoted as ( n^{th} ) root, where ( n ) indicates the degree of the root. The most common roots are square roots (2nd roots) and cube roots (3rd roots), but roots can exist for any integer ( n ).
The Concept of 3.4 as a Root
When we talk about 3.4 as a root, we are often referring to it in the context of the nth root. For instance, finding whether 3.4 is the square root of a number involves squaring it:
[ 3.4^2 = 11.56 ]
This means that 11.56 has a square root of 3.4. Similarly, you could investigate cube roots:
[ 3.4^3 = 39.304 ]
This suggests that 39.304 has a cube root of 3.4. Understanding how 3.4 behaves as a root aids in various applications in algebra and calculus, particularly when it comes to solving equations and modeling real-world phenomena.
Applications of Roots in Mathematics
1. Solving Equations
Roots are crucial in solving polynomial equations. Consider the equation ( x^2 – 11.56 = 0 ). By determining the roots, we can find the solutions to this equation. Roots simplify complex equations, allowing mathematicians to break down various expressions into simpler components.
2. Data Analysis
In advanced statistics, roots are often used in regression analysis and models for predicting data trends. For example, when dealing with datasets that follow a nonlinear pattern, transforming data using roots allows statisticians to linearize relationships. Let’s look at a practical example:
| Dataset Value | Transformed Value using Square root |
|---------------|-------------------------------------|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
This transformation facilitates easier handling of data, particularly in predictive modeling.
3. AI Gateway and Transformation of Data Formats
In today’s data-driven world, the intersection of mathematics, statistics, and technology is more significant than ever. Tools like an AI Gateway allow organizations to not only access AI-powered tools for analysis but also seamlessly integrate these tools into their data workflows.
AI systems often require data in specific formats, hence data format transformation becomes a necessary step. For mathematical computations involving roots, being able to manipulate data formats using APIs is critical.
Using a framework such as træfik, which is a modern HTTP reverse proxy and load balancer that makes deploying microservices easy, we can consider how this interaction enhances mathematical computational tasks.
In this context, APIs can facilitate consistent data requests to extract or manipulate numerical data involving roots, ensuring that mathematical computations are accurate and up-to-date.
Integrating AI and API Management in Mathematical Modeling
By leveraging APIs to call upon AI services, data scientists and mathematicians can automate complex calculations, including those involving roots like 3.4. Through a streamlined process involving API calls and the ability to adjust data formats at will, professionals can focus their efforts on interpretation rather than the raw calculation.
Setting Up API Calls for Mathematical Functions
As a practical example, let’s say you want to use an API to calculate the nth root of a number. Here’s a simple code snippet using curl to demonstrate how one might structure an API call:
curl --location 'http://api.mathservice.com/nth-root' \
--header 'Content-Type: application/json' \
--data '{
"number": 39.304,
"root": 3
}'
In this hypothetical example, the API will return ( 3.4 ) as the 3rd root of ( 39.304 ). This kind of setup bolsters efficiency in solving mathematical equations by allowing users to formulate specific requests against a backend that performs computations using well-established mathematical principles.
The Importance of Understanding Roots in Education
Understanding roots, particularly numbers like 3.4, is imperative in mathematics education. Here’s why:
-
Foundation for Advanced Concepts: Grasping the concept of roots lays a foundation for more advanced topics in algebra, calculus, and mathematical modeling.
-
Real-Life Applications: Roots are not merely abstract concepts; their applications range from engineering to economics. For instance, calculating areas, volume, and financial models often includes roots.
-
Fostering Critical Thinking: Recognizing patterns and solving equations that involve roots promotes critical thinking and problem-solving skills.
As educators emphasize these concepts, integrating technology and methodologies involving AI Gateways and API systems may also enrich the learning experience for students, providing them with tools to visualize and apply mathematical concepts in real-time.
Conclusion
The significance of 3.4 as a root in mathematics extends beyond mere numerical values. It pervades various applications in solving equations, analyzing data, and utilizing modern technology to further enhance our computational skills. As we move into an era dominated by digital solutions, integrating AI and API management to operate within mathematical frameworks will undoubtedly encourage innovation and efficiency in both academic and practical settings.
Understanding the concepts of roots and their significance serves as a gateway into deeper mathematical inquiries and applications. Through collaborative tools made available by advancements in technology, the exploration of mathematical principles will continuously evolve, inspiring future generations of mathematicians and data scientists.
To encapsulate, roots, especially specific values such as 3.4, play a crucial role in mathematics, impacting how we perceive and utilize numerical data in practical contexts. By synergizing these mathematical principles with technological tools, we cultivate an environment ripe for discovery and innovation.
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
In summary, maximizing the interplay between mathematical roots and technological solutions not only enhances computational efficiency but also reinforces the importance of fundamental mathematical concepts in contemporary applications. Through understanding and leveraging roots effectively, whether through traditional equations or modern AI frameworks, we can further drive our comprehension and application of mathematics in everyday life.
🚀You can securely and efficiently call the Tongyi Qianwen API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
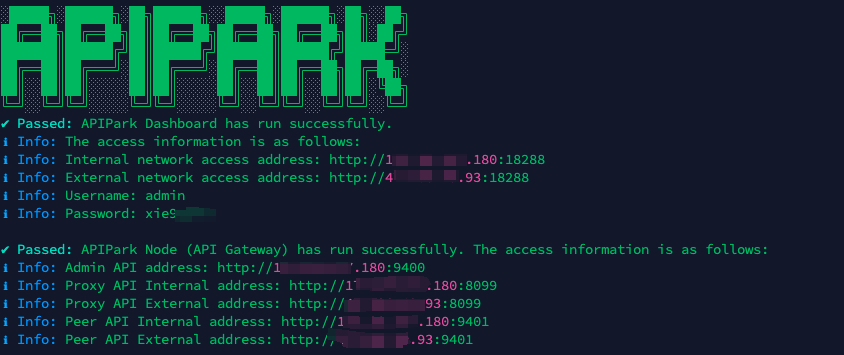
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
Step 2: Call the Tongyi Qianwen API.