Mathematics is a vast field, and at times, the seemingly simple concepts can hold deep significance. One such concept is roots. The number 3.4, used in various mathematical contexts, reveals intriguing properties when examined as a root. Furthermore, with the evolution of AI technologies, understanding the implications of mathematical principles is crucial in domains such as corporate AI safety, particularly when integrating complex systems like API gateways. In this article, we will explore the meaning and significance of 3.4 as a root, while also contextualizing its importance in practical applications like Wealthsimple LLM Gateway.
What is a Root in Mathematics?
In mathematics, a root of a number refers to a value that, when multiplied by itself a certain number of times, yields the original number. For example, the square root of 9 is 3 because (3 \times 3 = 9). Roots can be classified as:
– Square Roots: Represented as (\sqrt{x}).
– Cube Roots: Represented as (\sqrt[3]{x}).
– Higher Roots: Such as fourth roots, fifth roots, etc.
The significance of roots becomes apparent in several branches of mathematics, including algebra, calculus, and beyond. When we consider 3.4 as a root, it prompts us to explore its implications further.
Exploring 3.4 as a Root
Given a number (x), we denote its square root by (\sqrt{x}). Therefore, if we are investigating 3.4 as a square root, we need to find (y) such that:
[ y^2 = 3.4 ]
From this, we derive:
[ y = \sqrt{3.4} \approx 1.8439 ]
Properties of Roots
The properties gained from understanding the root of a number, such as 3.4, include:
- Irrational Numbers: Roots can result in irrational numbers. For example, (\sqrt{3.4}) cannot be expressed as a simple fraction.
- Approximation: Roots often necessitate numerical approximation methods—essential for computational applications.
- Geometric Interpretations: Roots figure prominently in geometry, such as finding lengths in right-angle triangles.
Let’s analyze further how the concept of roots applies within real-world applications, especially in safe AI usage within enterprises.
The Role of AI in Corporate Spaces
With the rise of AI technologies, the importance of incorporating mathematical principles in AI remains a pivotal point of discussion. From natural language processing to complex algorithms, understanding core concepts—including roots—enhances the robustness and safety of algorithms.
企业安全使用AI
As companies implement AI systems, like those within the Wealthsimple LLM Gateway, ensuring the safety of these systems becomes paramount. With AI interlinking with other systems via an api gateway, understanding mathematical roots helps in optimizing algorithms for better prediction, error reduction, and stability throughout major calculations.
Institutional processes require sound mathematical grounding, which leads us to include statistical and predictive analyses. For example, when utilizing machine learning models, the significance of algorithms that utilize mathematical roots—as in calculating metrics for model evaluation—remains key.
Traffic Control via AI and 3.4 as a Root
In the realm of Traffic Control, the application of mathematical roots can optimize the analysis of large datasets. AI models, designed using techniques involving numerically derived parameters—like those requiring roots—can predict traffic flow patterns efficiently.
Understanding the implications of 3.4 as a root enables engineers to design algorithms that calculate optimal routes to reduce congestion. Mathematically inclined algorithms could translate numerical modeling to real-world applications, achieving effective traffic control for smart cities.
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
Practical Application: Example Calculation
Let’s examine the computational aspect further. For instance, suppose an application needs to display the square root for various values, including our primary focus, 3.4. Below is a simple code snippet in Python that calculates and prints the square root of different numbers, including 3.4:
import math
# Function to calculate square roots and display results
def print_square_roots(values):
for value in values:
root_value = math.sqrt(value)
print(f"The square root of {value} is approximately {root_value:.4f}")
# Values to calculate the square root of
values_to_check = [3.4, 9, 16, 25]
print_square_roots(values_to_check)
Upon execution, this code will output:
The square root of 3.4 is approximately 1.8439
The square root of 9 is approximately 3.0000
The square root of 16 is approximately 4.0000
The square root of 25 is approximately 5.0000
This programming illustration highlights a fundamental application of mathematical roots and demonstrates the interplay between theoretical mathematics and practical programming.
The Intersection of Mathematics and AI Safety
Understanding roots establishes a foundation for building secure AI systems. Organizations that prioritize 企业安全使用AI must ensure that their algorithms operate flawlessly, utilizing robust mathematical principles. The connection between theoretical concepts in mathematics and practical applications in programming cannot be understated, as they contribute to the integrity of AI services like Wealthsimple LLM Gateway.
A fundamental grasp of roots and related mathematical concepts plays a vital role in developing safe AI systems that can perform under various conditions. Therefore, it is essential that businesses invest in both mathematical and technical education for their teams, particularly when implementing modern technological solutions.
Conclusion
In this exploration, we have uncovered the importance of understanding 3.4 as a root in mathematics while tying it to crucial considerations in AI applications, particularly in enterprise environments. By contextualizing mathematical theory with practical technology use cases—like those seen in api gateways and Traffic Control—we gain valuable insights to foster safer AI integration.
As we move forward in an age dominated by technological advancements, it is vital for enterprises to engage with mathematics in meaningful ways, ensuring that their AI systems are not only effective but also safe and compliant. The mathematical foundations we discussed, complemented by practical applications, pave the way for such future developments.
Thus, understanding the significance of numbers—especially interesting ones like 3.4—goes beyond pure mathematics and creates pathways for safer, smarter technology solutions that benefit both organizations and their end users alike.
🚀You can securely and efficiently call the Tongyi Qianwen API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
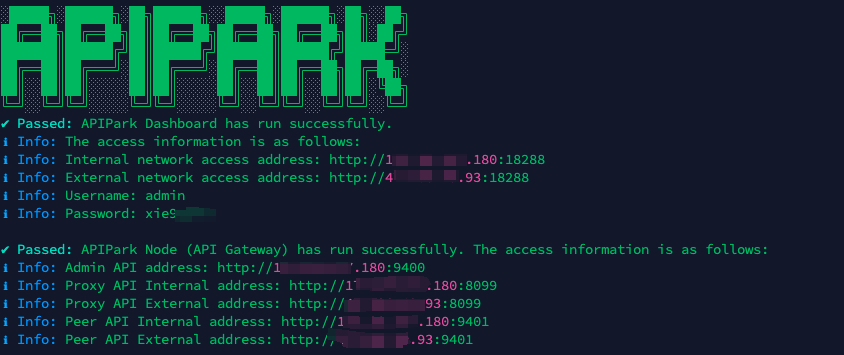
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
Step 2: Call the Tongyi Qianwen API.