Mathematics, often perceived as a realm for mere calculations and numbers, encompasses profound concepts that expand our understanding of various scientific fields. One intriguing concept is the idea of a number being a “root,” particularly focusing on 3.4 as a root. This article aims to explore the mathematical significance of 3.4 as a root, providing insights into its properties, applications, and connections to contemporary technologies such as the use of API calls in AI services including the Lunar.dev AI Gateway and LLM Gateway open source tools.
Table of Contents
- Mathematical Foundations of Roots
- The Concept of 3.4 as a Root
- Exploring Roots in Algebra and Beyond
- Practical Applications of Roots
- Integrating Technology: API Calls and AI Services
- Visualizing 3.4 as a Root: Diagrams and Representations
- Conclusion
Mathematical Foundations of Roots
To understand 3.4 as a root, we first embark on a journey into the foundational concepts of roots in mathematics. A root of a number ( x ) is another number ( r ) such that when multiplied by itself a given number of times (i.e., raised to the power of ( n )), it equals ( x ). Mathematically, this can be represented as:
[
r^n = x
]
The most common roots are square roots, cube roots, and higher-order roots. For instance, ( r ) being the square root means ( r^2 = x ); similarly, if ( r ) is a cube root, then ( r^3 = x ).
Key Properties of Roots
- Non-negativity: In the real number system, the principal square root is always non-negative.
- Existence and Uniqueness: Each positive number has exactly one non-negative square root. This principle holds true for other roots as well.
- Rational and Irrational Roots: Some roots, such as ( √2 ), are irrational, that is, they cannot be expressed as a simple fraction, while others are rational.
The Concept of 3.4 as a Root
When we specifically discuss 3.4 as a root, we need to determine the value of ( x ) and ( n ) that satisfies the equation ( r^n = x ). Therefore, deciding whether we are looking at 3.4 as a square root, cube root, or higher power root is crucial.
Example: 3.4 as a Square Root
If we consider 3.4 as the square root of some ( x ), then:
[
3.4^2 = x
]
Calculating this:
[
x = 3.4^2 = 11.56
]
Thus, 3.4 is the square root of 11.56. This means that the significance of 3.4 lies in its ability to simplify or define relationships in quadratic equations and functions.
Example: 3.4 as a Cube Root
If we now think of 3.4 as a cube root, the equation transforms to:
[
3.4^3 = x
]
Calculating this gives:
[
x = 3.4^3 = 39.304
]
Consequently, 3.4 represents the cube root of 39.304, making it essential in the study of cubic functions and various real-world applications like volume calculations.
Exploring Roots in Algebra and Beyond
Algebra extensively utilizes roots in an array of calculations — from solving equations to simplifying expressions. For instance, when solving a quadratic equation of the form:
[
ax^2 + bx + c = 0
]
The roots (solutions) can be found using the quadratic formula:
[
x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}
]
In cases where the discriminant ( b^2 – 4ac ) is positive, we end up with two distinct real roots. If it is zero, we have one real root, and if negative, the roots are complex.
The Role of Roots in Function Analysis
Roots of functions are variables that make the function equal to zero. Understanding where these roots occur allows for greater insight into function behavior, local minima and maxima, and inflection points — all pivotal in fields like calculus.
Practical Applications of Roots
The applications of roots extend well beyond theoretical mathematics. They play a critical role in various fields such as:
- Physics: For instances involving wave functions or harmonic motion.
- Engineering: Calculating load distributions through square and cube roots.
- Finance: Using roots to evaluate growth rates and compound interest equations.
A notable application of roots can be observed in geometry, especially in calculating areas and volumes associated with different shapes, as well as in statistical analyses involving standard deviations.
Integrating Technology: API Calls and AI Services
In the modern era, the integration of mathematics with technology has proliferated, particularly through API calls that enable intercommunication between software applications. As businesses and developers leverage AI capabilities, tools like Lunar.dev AI Gateway and LLM Gateway open source become essential.
Utilizing API Calls to Extract Mathematical Functions
APIs allow us to harness the power of AI models that can calculate roots and other mathematical functions with ease. Below, we will demonstrate an API call to use the Lunar.dev AI Gateway for calculating the roots of given numbers.
Example of API Call in Bash
curl --location 'http://lunar.dev/api/calculate' \
--header 'Content-Type: application/json' \
--header 'Authorization: Bearer YOUR_API_TOKEN' \
--data '{
"number": 3.4,
"operation": "square_root"
}'
In this example, we assume YOUR_API_TOKEN is replaced with a valid token for authentication. Such API calls can significantly reduce manual calculations and provide various mathematical solutions, enhancing productivity in data-heavy environments.
Visualizing 3.4 as a Root: Diagrams and Representations
To encapsulate the concept of 3.4 as a root, diagrams and visual representations can significantly aid understanding. Below is a diagram illustrating the relationship between the root, its various powers, and the resultant values.
Diagram Representation
| Root Type | Expression | Result |
|---|---|---|
| Square Root | ( 3.4^2 ) | 11.56 |
| Cube Root | ( 3.4^3 ) | 39.304 |
This table provides a quick reference for understanding how changing the root or power affects the resultant value, showcasing the fundamental connection between roots and their corresponding outputs.
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
Conclusion
The exploration of 3.4 as a root unveils numerous mathematical principles and applications. From algebra to real-world modeling, understanding the roots and their implications is vital for advancing in mathematics and its associated disciplines. Coupled with innovative technologies such as API calls and AI integration, the future of mathematical computation appears boundless, paving the way for smarter, more efficient problem-solving experiences. The journey into the world of roots is not merely a mathematical endeavor but a gateway to a broader understanding of relationships within mathematics and technology.
🚀You can securely and efficiently call the Anthropic API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
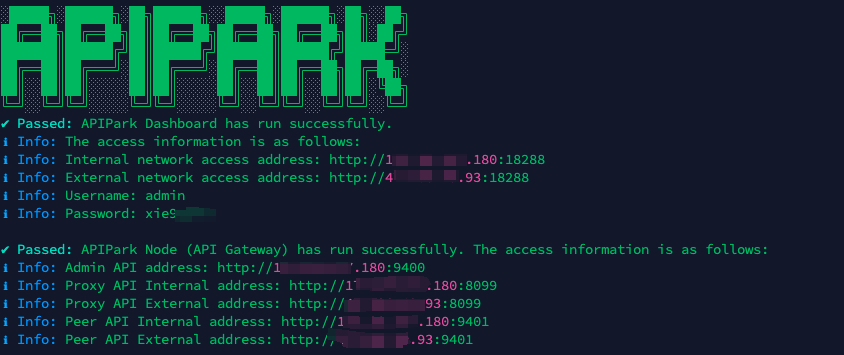
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
Step 2: Call the Anthropic API.